FHE 是計算的聖盃,價值和計算正在向開放、無需許可的網路過渡,FHE 將支撐大部分所需的基礎設施和應用程式。本文源自 Evan Fisher & Vikramaditva Singh 所著文章 《Fully Homomorphic Encryption》,由 深潮TechFlow 編譯、整理。
(前情提要:詳解》為什麼以太坊需要「共識層ZK化」 )
(背景補充:zkSci:零知識證明如何結合科學研究? )
隨著市場在熊市中的沉寂,投資者和專案方總會開始尋找新的成長點。
在缺乏持續性熱點的空窗期,正是探索和深入瞭解新技術的絕佳機會,因為新技術可能會成為下一個市場敘事的核心。
上個月,知名的加密風投公司 Portal Ventures 在其官方部落格上釋出了一篇詳細探討全同態加密(FHE)技術的文章。然而,這篇深入的技術文章似乎並沒有引起大眾的廣泛關注。

Portal Ventures 的作者這樣說到:
“全同態加密是加密方案的聖盃 “。
理解 VC 關注的技術對於投資者來說至關重要,因為它可以幫助我們預測和理解下一個市場週期的潛在趨勢。事實上,同態加密、零知識證明和多方安全計算等技術在密碼學領域都有深遠的影響,尤其是全同態加密,它在加密貨幣和 web3 領域可能都有巨大的應用潛力。
但問題是,大多數人對於全同態加密的真正意義、如何工作以及與其他技術的區別都知之甚少。在市場不景氣,投資情緒低迷的時候,跳出炒作的喧囂,深入研究和了解這些前端技術,無疑是一個明智的選擇。
有些巧合的是,筆者在數年前有幸在工作中接觸過與 FHE 相關的技術解決方案。因此決定對 Portal Ventures 的這篇文章進行深入的解讀,希望為大家提供一些新的視角和思考。
同態與全同態加密,到底是個啥?
如果直接看 Portal Ventures 的原文,您可能會對全同態加密(FHE)的複雜數學描述感到困惑。
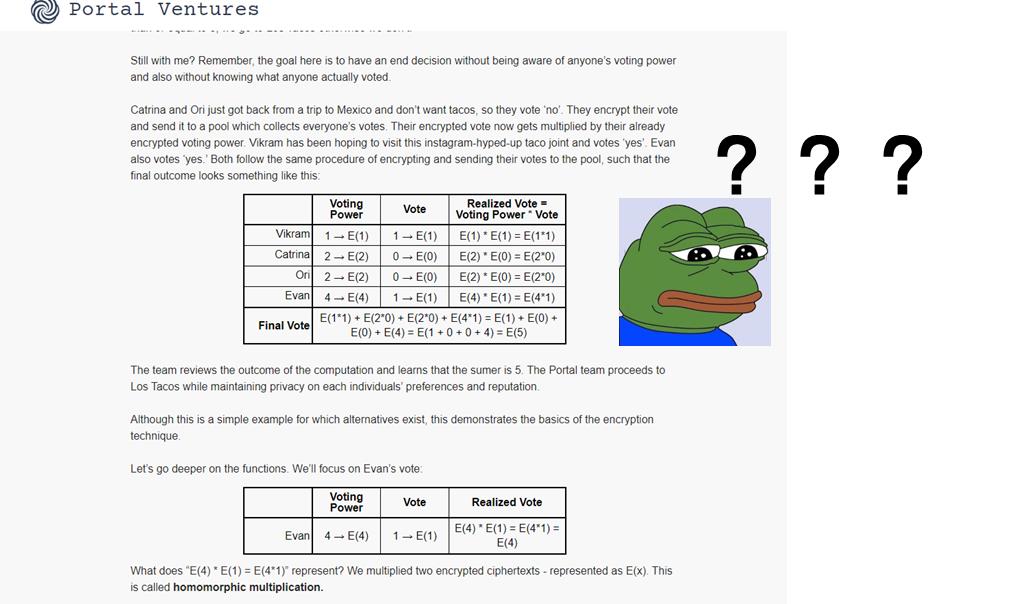
事實上,密碼學的世界充滿了深奧和技術性,但我們完全可以用簡單和通俗的方式來解釋這些概念。在這一節中,筆者試圖為您提供一些更直觀、更易於理解的例子,幫助您深入瞭解全同態加密。
首先,想像一個 「祕密魔盒」。您可以將任何物品放入這個盒子,並鎖定它。一旦鎖定,您就不能看到或觸控盒子裡的內容。但是,令人驚奇的是,這個魔盒允許您在不開啟它的情況下,改變裡面物品的顏色或形狀。
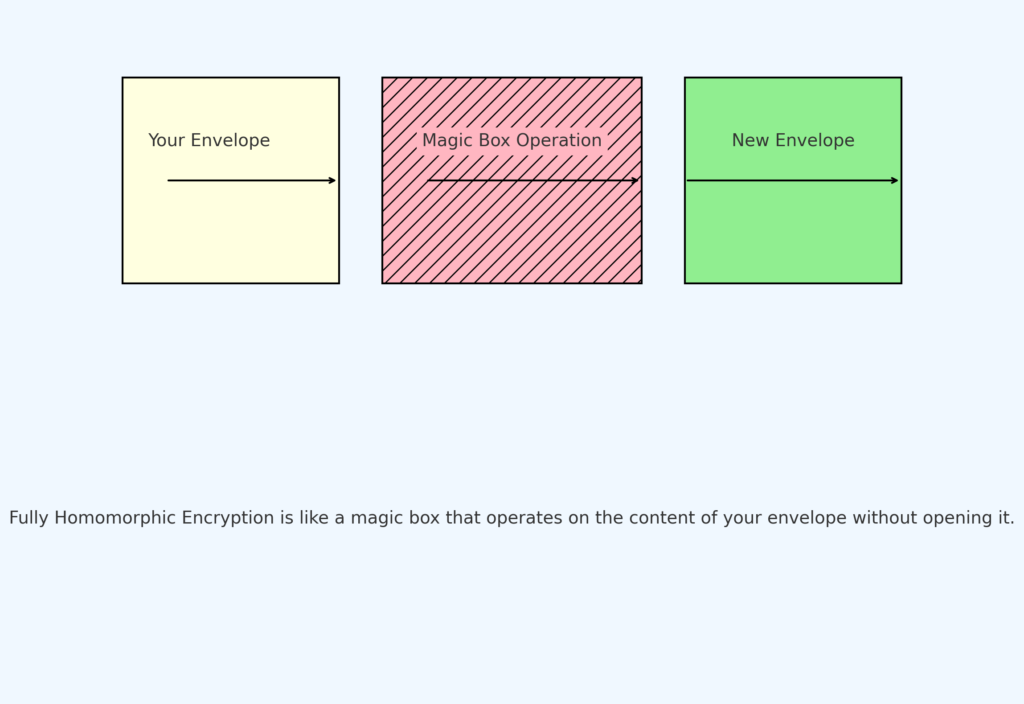
如上圖所示,全同態加密(Fully Homomorphic Encryption)可以被視為一個魔法盒子:
- 你的信封 (Your Envelope): 這代表你想加密的原始資料。
- 魔法盒子操作 (Magic Box Operation): 即使不解密或開啟信封,你也可以在信封裡的資料上進行操作(如加、減等計算)。
- 新的信封 (New Envelope): 經過魔法盒子操作後,你會得到一個新的加密結果。
這就是同態加密的基本思想: 在不瞭解資料本身的情況下,也能對加密的資料進行操作。
這個通俗的例子有助於搞清楚 “全同態加密” 在幹什麼。但實際上,這個概念本身還是有點聽君一席話如聽一席話。那麼,什麼又叫做 「全」 和 「同態」?
什麼叫做 「全」(Fully)?
- 在密碼學中,加密方案可以支援多種操作,比如加法、乘法等。當我們說一個加密方案是 「全同態」 的,我們意味著這個加密方案支援在加密資料上進行任意數目的基本運算(例如加法和乘法)而不需要解密。這與部分同態加密(如只支援加法或只支援乘法的方案)形成對比。
什麼叫做 「 同態 」( Homomorphic )?
- “同態” 來自於希臘文,意思是 「相同的形狀或結構」。在密碼學中,當我們說加密方案是同態的,意味著有些運算在明文上的效果與在密文上的效果是一樣的。換句話說,如果你在加密的資料上進行某種運算,然後解密結果,這和你先解密資料然後在解密後的資料上進行相同的運算是等價的。
例如,考慮一個支援同態加法的加密方案。假設你有兩個數位:3 和 4。你可以先加密這兩個數位,然後使用這個同態加密方案將兩個加密的數位相加。最後,你解密相加後的結果。得到的解密結果將是 7,這與你直接在明文 3 和 4 上相加得到的結果是一樣的。
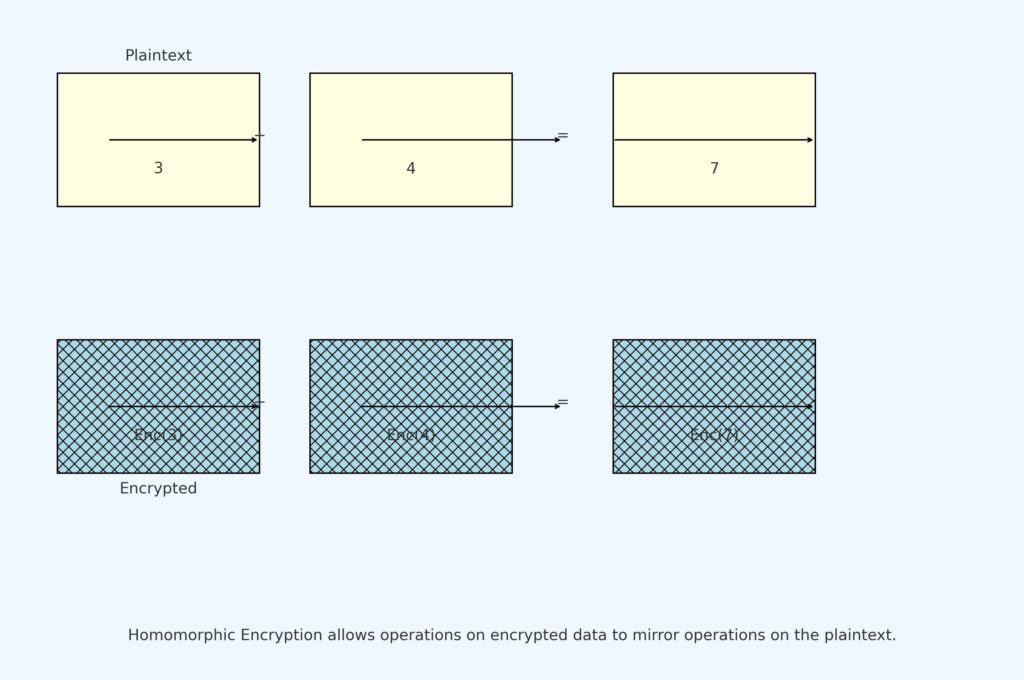
但是,您可能會問,我們如何在非數位上進行這些加減乘除操作呢?實際上,我們可以使用特定的編碼方法將非數位資料轉化為數位形式,從而在它們上進行加法和乘法等運算。這意味著全同態加密的應用不僅僅限於數學計算,它還可以被廣泛應用於其他領域。
為了更直觀地解釋這個概念,讓我們考慮醫療資料的例子。
- 假設醫院有一些患者資料,比如年齡和血糖值,但出於隱私考慮不希望直接傳送給雲服務提供商進行分析。
- 通過使用全同態加密,醫院可以先將這些資料加密。
- 想像一下,雲服務提供商需要計算所有患者的平均年齡(這需要加法和除法)和血糖值的總和與患者數量的乘積(這涉及加法和乘法)。
- 所有這些計算都可以在加密的資料上完成,而無需解密。雲服務提供商在不解密資料的情況下完成計算,然後將加密的結果返回給醫院。這確保了資料的隱私,同時也滿足了資料處理的需求。
這就是全同態加密的魅力所在,它為我們提供了一個既安全又靈活的資料處理方法。
為何 FHE 很重要?
當前,對加密資料進行計算的現有方法並不理想。它們在資源使用和時間消耗上都相對昂貴。
因此,行業標準流程是,在進行計算之前,由第三方(即公司)對資料進行解密。
以一個具體的例子來說,想像一下您有一個數據檔案,其中包含一些高調個體的財務資訊。
- 我們稱這個檔案為 「M」。我們需要某個公司對這些資料進行分析。
- 目前的流程是怎樣的呢?首先,我使用如 RSA 或 AES 這樣的加密函式對 M 進行加密。此時,M 變成了 E (M),其中 E 是加密函式。
- 接下來,我將 E (M) 傳送給公司伺服器。公司現在通過相關的解密函式 D 來解密 E (M) 為明文,即 D (M)。
- 公司直接對檔案 M 進行明文進行分析操作。
- 操作完後,再把 M 加密一次,生成一個 E (M’)。
- 公司再把加密的 M’ 並將其傳送回給我,然後我再次解密它。

發現了嗎,這裡的關鍵問題在於,當公司解密 M 並將其儲存在其伺服器上進行計算時, 第三方可以訪問原本應受保護的敏感資料。如果該人員遭到駭客攻擊或有惡意意圖,這就會引發問題。
全同態加密(FHE)通過允許對加密資料進行計算來解決此問題。公司不再需要解密 E (M)。它直接在加密資料上進行分析。沒有解密的需要,也不需要信任假設。
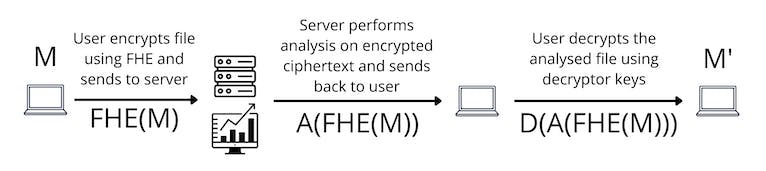
綜上所述,全同態加密的引入解決了當前資料處理流程中的一個關鍵問題,即在第三方處理資料時可能暴露的隱私風險。FHE 為我們提供了一個在保證資料隱私的同時,有效地處理加密資料的方法。
FHE 在 Crypto 中如何應用?
全同態加密(FHE)為加密世界開啟了一扇新的大門,為我們帶來了許多之前無法想像的應用場景。Poly Venture 的原文對場景的描述比較簡單,我們試著用一張表更有條理的做出了一個解讀。
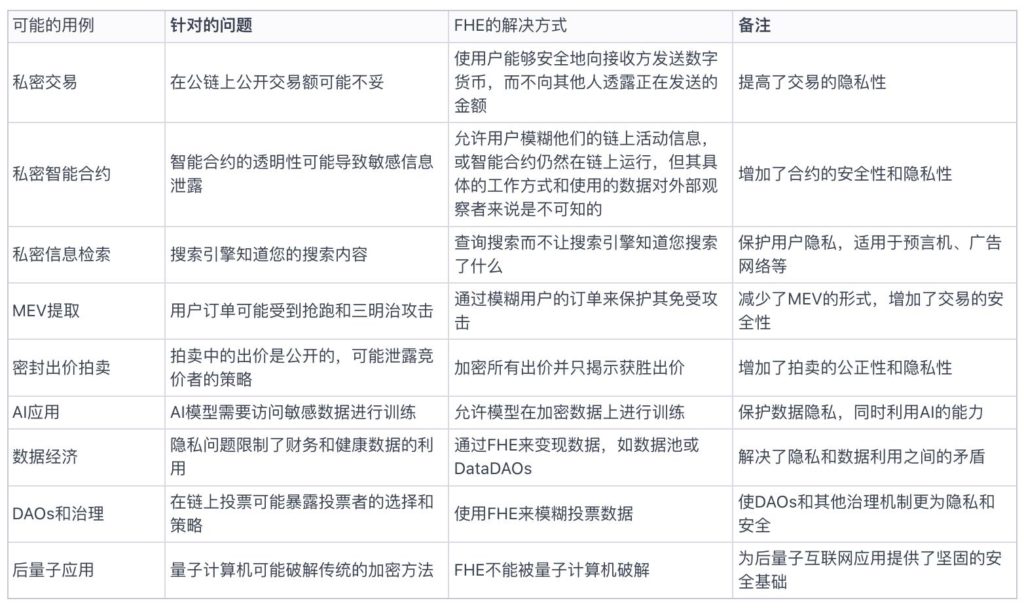
FHE vs ZK vs MPC,傻傻分不清?
在瞭解了全同態加密(FHE)後,很容易將其與其他熟悉的技術,如零知識證明(ZK)和多方計算(MPC)相提並論。乍一看,它們似乎都致力於解決相似的隱私和計算問題。但這三者之間實際上有哪些聯絡和區別呢?
首先,我們先了解一下這三種技術的基本定義:
- FHE :允許在加密資料上執行計算,而無需解密。
- ZK : 允許一方向另一方證明某個陳述是真實的,而無需揭示任何關於該陳述的具體資訊。
- MPC : 使多方能夠共同在他們的私有資料上執行計算,而不向其他參與者洩露輸入資料。
然後,讓我們從多個維度來看看他們的異同和交集:
目的:
- FHE 的主要目的是在 不解密的情況下 進行計算。
- ZK 的目標是 證明一個事實的正確性 而不洩露有關該事實的任何資訊。
- MPC 的目標是 允許多方安全地共同計算 ,而不洩露各自的輸入。
隱私與計算:
- 在 ZK 中,計算不一定是私有的。例如,儘管你可以使用 ZK 來驗證銀行帳戶餘額是否超過 100,000 美元,但進行這樣的驗證的計算不一定是私有的。
- 與此相反,FHE 確保了計算的隱私性,因為所有的計算都在加密資料上進行。
限制與挑戰:
- MPC 需要至少一個誠實的伺服器,並且可能受到 DDoS 攻擊、沉默合謀攻擊和通訊開銷的影響。
- ZK 主要用於證明正確性,而不是隱私技術。
- FHE 儘管提供了強大的隱私,但計算效率較低,對資源的需求較大。
在加密領域的應用 :
- FHE 可以用於構建更加隱私的智慧合約和其他區塊鏈應用。
- ZK 被用於建立可擴充套件的區塊鏈解決方案,如 zk-rollups。
- MPC 主要用於私鑰管理和託管。
交叉使用:
- MPC 可以與 FHE 結合,形成閾值 FHE,通過將一個 FHE 加密金鑰分割成多個,並給每個參與者一個來增強安全性。
- zkFHE 是零知識證明和全同態加密的結合,正在被研究,以實現在 FHE 智慧合約上的 zk-rollups。
總體來說,儘管 FHE、ZK 和 MPC 在某些方面有所重疊,但它們都有各自獨特的優勢和應用場景。在加密世界中,這三種技術都為增強隱私和安全性提供了巨大的潛力,但它們的結合和進一步的研究仍然是加密社群的一個活躍領域。
最後,我們也可以給出一張省流版的表格,將上述技術放在一起進行比較,幫助大家更加直觀的進行理解。
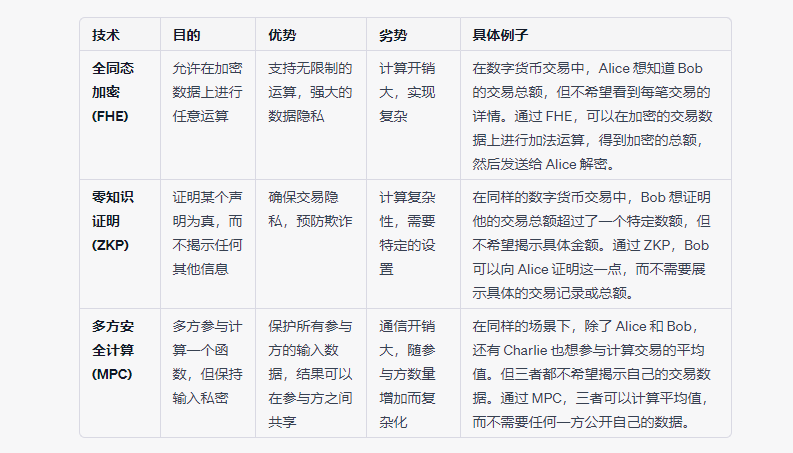
FHE 的未來展望
通過上文可以感覺到,全同態加密(FHE)顯然是一種強大的技術。
但為什麼它還沒有被廣泛採用,甚至在加密 CT 中很少提及?一方面由於理解技術本身有一定門檻,另一方面則在於 FHE 技術目前還面臨一些挑戰,難以輕鬆以商業化形態走進大眾視野。
面臨的挑戰可能有:
- 計算密集 :當我們的密文互相作用時,為了維持安全性,會新增更多的噪聲。FHE 方案使用 「自舉」 技術來減少噪聲,但這非常計算密集,資源消耗很大。
- 功能有限: FHE 的計算僅限於加法、乘法及其變種 / 組合。例如,不能在 FHE 中使用 if 語句,因為內容是加密的。此外,構建相對複雜的操作,如比較和除法,需要仔細規劃基本邏輯,這導致了更複雜的程式設計技巧和計算效率較低。
- 相容性 / 組合性問題 :現有的應用程式和服務提供商並不是為了在加密資料上進行計算而構建的。這限制了 FHE 與現有技術的整合,並增加了開發 FHE 相容應用所需的慣性。
可能的解決方案:
- 硬體加速器 :某些 FHE 方案,如 nuFHE 和 cuFHE,可以使用 GPU 加速,但主要的突破將來自更快的 FPGA 和 ASIC。其他技術,如光子技術,也正在被研究,以加速 FHE 的硬體用例。
- 新的程式設計正規化 :就像在 Python 上用於複雜數學的包如 pandas 和 numpy,FHE 庫也將被構建。目前,Zama 和 Sunscreen 是兩個為 FHE 構建此類庫和 SDK 的專案。此外,還需要構建專門的編譯器,以使開發人員能夠統一 FHE、ZKP 和 MPC。
- FHE 與現有解決方案之間的整合 :將構建解決方案,使現有工具與 FHE 相容,作為工具和 FHE 加密資料之間的中間層。
最後,Portal Ventures 在原文的結論部分再次強調:
「FHE 是計算的聖盃,我們正在接近它的商業化。價值和計算正在向開放、無需許可的網路過渡,我們相信 FHE 將支撐大部分所需的基礎設施和應用程式」。
此外,它們也表達了對於目前正在研究 FHE 的專案的興趣。因此,我們可以看到的是,VC 對 FHE 有興趣,或者說 VC 會率先對尚未走進大眾視野的硬核技術感興趣。
歷史表明,基於新技術的加密專案,往往都帶有閃亮的光環和較高的估值,並且受到各路資本的追捧。
在下一場盛宴開始前,我們的確應該多花時間,提前研究入場嘉賓的身份,才能在宴會開始時應對自如。






